倒排索引_Inverted_Indexing

发表于 | 分类于

Definition of an Inverted index

An inverted index is typically composed of a vector containing all distinct words of the text collection in lexicographical order (which is called the vocabulary) and for each word in the vocabulary, a list of all documents (and text positions) in which that word occurs

通俗的说: 单词到包括该单词的文档的集合的映射。

注释: 这里的单词可能是被处理过的，一些常用的处理方法有

  • Case folding: converting all uppercase letters to lower case
  • Stemming: reducing words to their morphological root
  • Stop words: removing words that are so common they provide no information

Inverted index 的应用情景

假设有这样一个Query:

1
Which plays of Shakespeare contain the words Brutus AND Caesar but NOT Calpurnia?
方法一 暴力搜索

先找到所有包含Brutus和Caesar的话剧，再逐字排查，如果含有Caplurnia就删除掉该话剧。

缺点：

  • Too slow
  • 需要很大的空间
  • 不够灵活，不支持其他的操作，比如”Find the word Romans near countrymen”
方法二： Term-Document Incidence Matrix

用了 Bit Map 位运算的思想。构建如下矩阵，(t,d)=1代表term t在document d中出现，0代表没有出现。例如：

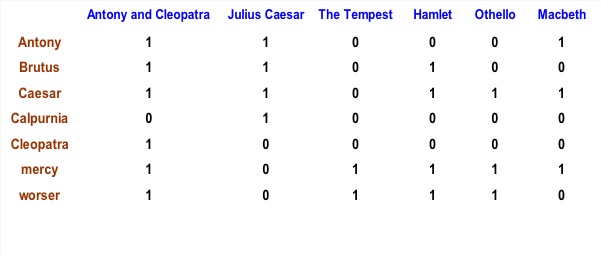
image

这样对于上一个查询，只需要

110100 AND 110111 AND 10111 = 100100

所以the two plays matching the query are:

“Anthony and Cleopatra”, “Hamlet”

缺点：

  • 需要很大的空间,并且矩阵通常十分稀疏:
1
2
3
Given 1 million documents and 500,000 terms.
The (term x Document) matrix in this case will have size 500K x 1M or
half-a-trillion 0’s and 1’s.
方法三： Inverted Index

在数据结构上我们选择了链表而不是数组，链表的优势在于：

  • Dynamic space allocation
  • Insertion of terms into documents easy
  • There is space overhead of pointers, though this is not too serious

Inverted Index的构建如下图所示
image
image

应用举例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
1）Brutus AND Caesar
- Locate Brutus in the Dictionary and Retrieve its postings.
Brutus: 2->4->8->16->32->64->128
- Locate Caesar in the Dictionary and Retrieve its postings.
Caesar: 1->2->3->5->8->13->21->34
- “Merge” the two postings and select the ones in common (postings are document ids):
Brutus: 2->4->8->16->32->64->128
Caesar: 1->2->3->5->8->13->21->34
2->8
O(m + n) 复杂度
2）Brutus AND Calpurnia AND Caesar
Brutus: 2->4->8->16
Caesar: 1->2->3->5->8->13->21->34
Calpurnia: 2->16
Merge的顺序要从短到长依次进行
Execute the query as (Calpurnia AND Brutus) AND Caesar.
INTERSECT(<t1, . . . , tn>)
   terms ← SORTBYINCREASINGFREQUENCY(<t1, . . . , tn>)
   result ← postings( first(terms))
   terms ← rest(terms)
   while terms /= NIL and result /= NIL
   do
       result ← INTERSECT(result, postings(first(terms)))
       terms ← rest(terms)
   return result
印象中有算法解决Merge K sorted list复杂度可以到nklogk(n为链表的平均长度）
[LeetCode参考: https://leetcode.com/problems/merge-k-sorted-lists/description/]
书本并没有采取这种算法可能有原因的：
- 在实际情况中这些个链表的长度一点也不平均
- 只需要最短的那个链表给merge结束就完事了我们并不需要完完整整的merge。

Skip Pointers

相关视频讲解

目的： speed up the merging of postings

方法解释：如图所示
image

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
INTERSECTWITHSKIPS (p1, p2)
	answer ← < >
	while p1 /= NIL and p2 /= NIL
	do if docID(p1) == docID(p2)
        then ADD(answer, docID(p1))
            p1 <- next(p1)
            p2 <- next(p2)
        else if docID(p1) < docID(p2)
                then if hasSkip(p1) and (docID(skip(p1)) <= docID(p2))
                     then while hasSkip(p1) and (docID(skip(p1) <= docID(p2))
                       do p1 <- skip(p1)
                    else p1 <- next(p1)
				else if hasSkip(p2) and (docID(skip(p2)) <= docID(p1))
                    then while hasSkip(p2) and (docID(skip(p2) <= docID(p1))
                       do p2 <- skip(p2)
                    else p2 <- next(p2)
	return answer

适用范围：

  1. Index 相对固定 update的次数比较少: Building effective skip pointers is easy if an index is relatively static; it is harder if a postings list keeps changing because of updates. A malicious deletion strategy can render skip lists ineffective.
  2. the presence of skip pointers only helps for AND queries, not for OR queries.

问题： How many skip pointers should we add?

  1. TradeOff Problem:
  • More skips -> shorter skip span => more likely to skip. But lots of comparision to skip pointers
  • Fewer skips -> few pointer comparision, but then long skip spans => few successful skips
  1. Simple Heuristic
  • 用Length的平方根: for a postings list of length P, use sqrt{P} evenly-spaced skip pointers.

硬件对速度的影响

Choosing the optimal encoding for an inverted index is an ever-changing game for the system builder, because it is strongly dependent on underlying computer technologies and their relative speeds and sizes. Traditionally, CPUs were slow, and so highly compressed techniques were not optimal. Now CPUs are fast and disk is slow, so reducing disk postings list size dominates. However, if you’re running a search engine with everything in memory then the equation changes again.

Phrase Queries

之前所说的inverted index技术是基于Term的，但是在实际运用中我们经常会查询一个短语，而不是单词，比如：stanford university

这里阐述两个方法

方法一： Bi-word indexes (2-grams, 2 shingles)

方法介绍

  • A bi-word (or a 2-gram) is a consecutive pair of terms in some text。比如 “Friends, Romans, Countrymen” 会生成 “friends romans” 和 “romans countrymen”
  • Each of these bi-words is now added to the dictionary as a term。也就是说之前的Term变成了现在的bi-words。

缺点

  • 数量爆炸！Bi-words will cause an explosion in the vocabulary database
  • 短语长度也许大于2。Queries longer than 2 words will have to be broken into bi-word segments
方法二： Positional indexes

方法介绍

相比于之前的inverted index, 这里其实就是多记录了一个Term出现的位置位置：

1
2
3
<Term, TotalFrequency> -> <docID, Frequency> 
变成
<Term, TotalFrequency> -> <docID, Frequency, Positions>

image

比方说我们要查询

1
to be or not to be

现在我们首先找to be, 步骤如下

1
2
3
4
5
1. 找到同时含有to和be两个term的文档。
2. 查找两个term在文档中的位置，如果be的位置在to后面一个，那就找到了一个结果
比如上面那个图，我们就能找到一个possible match是
to: <...;4:<...,429,433>;...>
be: <...;4:<...,430,434>;...>

算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
POSITIONALINTERSECT(p1, p2, k)
    answer <- <>
    while p1 /= NIL and p2 /= NIL
    do if docID(p1) == docID(p2)
        then l <- <>
            pp1 <- positions(p1)
            pp2 <- positions(p2)
            while pp1 /= NIL
            do while pp2 /= NIL
                do if |pos(pp1) - pos(pp2)| <= k
                    then ADD(l, pos(pp2))
                    else if pos(pp2) > pos(pp1)
                        the break
                    pp2 <- next(pp2)
                while l /= <> and |l[0] - pos(pp1)| > k
                do DELETE(l[0])
                for each ps in l
                do ADD(answer, <docID(p1), pos(pp1), ps>)
                pp1 <- next(pp1)
            p1 <- next(p1)
            p2 <- next(p2)
        else if docID(p1) < docID(p2)
            then p1 <- next(p1)
            else p2 <- next(p2)
    return answer