Digital Signature 数字签名

什么是数字签名

考虑这样的一个场景:
Alice 想给 Bob 发送一个信息。

• Alice把信息放在一个信封里
• Alice用自己的印章封住了信封

所有人都可以通过检查封印知道:
这封信来自于Alice,因为印章是Alice的。
同时可以通过查看封印是否完好得知信息有无被修改。

Digital Signature就是想实现同样的功能。

更贴近现实生活的一个例子是支票。

公钥和私钥对

在编码学中我们用公钥(Public Key)和私钥(Private Key)对来实现数字签名协议

• Priate key 用于签名(发送者才有, 不可以公开)
• Public key 用于验证(所有人都可以验证，是公开的)
• 每一个文件都有独特的签名(签名是跟着文件才生效的，就像日常中你不能把一个地方的签名减下来贴到另一个地方)

数字签名的工作流程

1. Create Keys

• Alice生成一定大小的私钥
• Alice用私钥生成公钥

1. Create Signature

• Alice用私钥给meesage签名
• Alice将签名, message和Public Key发送给Bob

1. Verify

• Bob用签名, message和public key验证Alice一定拥有对应的私钥。
• 因此Alice是一个友善的发出者

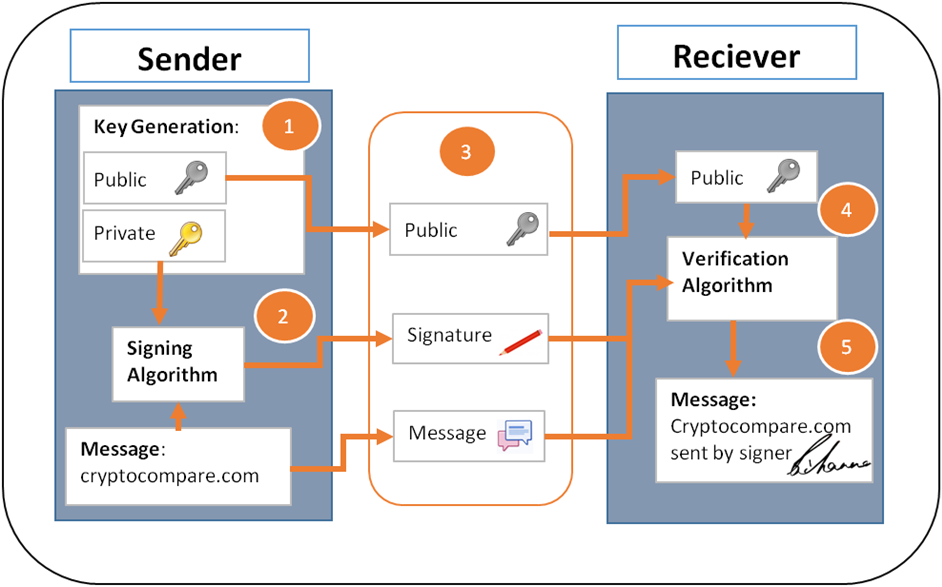
[图片来源: https://www.cryptocompare.com/wallets/guides/how-do-digital-signatures-in-bitcoin-work/]

ECDSA (Elliptic Curve Digital Signature Algorithm 椭圆曲线算法)

• What ECDSA does is to provide a method for computing a public key from the private key in a non-invertible fashion (也就是说，我们可以通过ECDSA算法计算出一个私钥对应的公钥，但是不能通过已知公钥算出对应的私钥-要找也只能Brute Force)
• Private key is a 256 bit long number chosen by Alice

Elliptic curves

An elliptic curve is represented algebraically as an equation of the form:
$$y^2 = x^3 + ax + b$$
For a = 0 and b = 7 (the version used by bitcoin), it looks like this:
$$y^2 = x^3 + 7$$

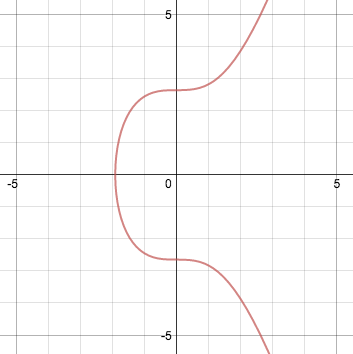
Elliptic curves有一些有用的特性

• 曲线上两个非切点的非垂直于坐标轴的连线必定与曲线相交于另一点
• 曲线上一点的不与坐标轴垂直切线一定与曲线相较于另一点。
  由此两个特性，可以定义如下运算。

Point addition, Point doubling and Scalar multiplication

1.Point addition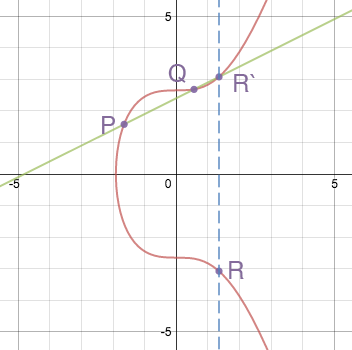

$$P+Q=R$$
P和Q连线与曲线交点关于x轴的对称点
2.Point doubling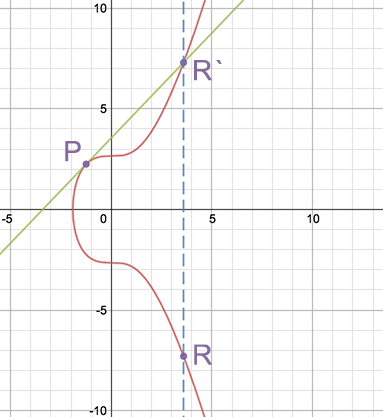

$$P+P=R$$
P的切线与曲线交点关于x轴的对称点
3.Scalar multiplication
计算$$R=7P$$并不需要7次加法。
$$R=7P=P+2(P+2P)$$
总共其实只需要4次运算。

Finite fields (有限域)

曲线是无限的，但是我们期望所得到的点是落在有限的区域里，最简单的方法就是模运算。
如图则是将x, y mod 67的结果。这样所有点都落在66*66的空间里（还是关于某个与原x轴平行的线对称的）

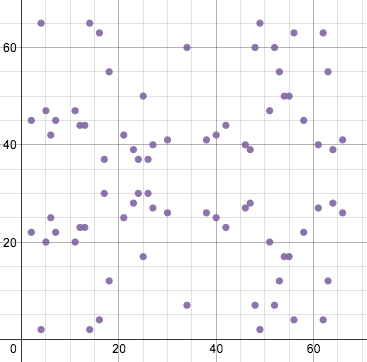
那么上述的加法操作要怎么进行呢?
采取的方法是保证两点连线的斜率不发生变化，水平和上下移动直到碰到一个点。
再取该点的对称点。如下图所示

签名步骤

• Base point G= 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
• public key = private key * base point
• Alice hashes the message. The hash is z.

签名过程

1. Choose some random (or deterministic) integer k between 1 and n - 1. (n is called order - FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141)
2. Calculate the point (x, y) = k * G, using ECDSA multiplication.
3. Find r = x mod n. If r = 0, return to step 1.
4. Find s = (z + r * d) / k mod n. If s = 0, return to step 1.
5. The signature is the pair (r, s)

验证

Q是public key, 其他字符和上面代表的一样

1. Verify that r and s are between 1 and n - 1.
2. Calculate w = s-1 mod n
3. Calculate u = z * w mod n
4. Calculate v = r * w mod n
5. Calculate the point (x, y) = uG + vQ
6. Verify that r = x mod n. The signature is invalid if it is not.

####参考资料

• https://www.coindesk.com/math-behind-bitcoin/
• http://www.ehcoo.com/Bitcoin_ECDSA.html

交易 - Transaction

一点点手写笔记

一个真实的交易

示例链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

{
   "ver":1,
   // List of inputs 数组
   "inputs":[
      {
         "sequence":4294967295,
         "witness":"",
         "prev_out":{
            "spent":true,
            "tx_index":283891696,
            "type":0,
            // Sender 发送地址
            "addr":"1GEpdQKniomEWNBT57i2Gakx3LbocdPbBu",
            // Amount 83252 Satoshis
            "value":83252,
            "n":0,
            "script":"76a914a7270d42995925700c222f8490d04beca9b8136388ac"
         },
         "script":"473044022050d8b9012569a81937e95922d0d731d9962da37ff68b3a91bad459c11a92e263022031981eec3e698cb078a69a09997c9384702524b251d574c413ff1847d6c498b60121039840b9ff142da071cd3fdb94fbf3460b0b6b8b5a7dad836a5586ee192ffbe520"
      }
   ],
   "weight":756,
   "block_height":485786,
   "relayed_by":"0.0.0.0",
   // List of outputs 数组
   "out":[
      {
         "spent":true,
         "tx_index":283891999,
         "type":0,
         // Receiver 接受地址
         "addr":"3BX3ev7igW8pzFV4GrkkAvaNv6wv5de4ns",
         "value":49992,
         // input index
         "n":0,
         //This scriptsig is a combination of the sender’s (后面还会说到multisig) signature and their public key
         "script":"a9146bce8af68361b1fbf6bd6cc2c08acf1705a10e0887"
      }
   ],
   // Lock Time 之后我们要介绍
   "lock_time":0,
   "size":189,
   "double_spend":false,
   // Receive Time
   "time":1505676139,
   "tx_index":283891999,
   // In counter, input的数量
   "vin_sz":1,
   // Transaction ID
   "hash":"e646284afca18a67980ba96cd3b891476fe182ef9235878296ac18091659440e", 
   // Out counter, output的数量
   "vout_sz":1
}

Lock Time

The locktime indicates the earliest time a transaction can be added to the blockchain.

想象一个实际生活中的场景: Alice给Bob一个支票，支票上写Bob只有到某个日期才能使用支票提款。在比特币中，我们则用Lock Time来实现这个Post Date

除此之外，Locktime给支付者了一定的反悔时间。

• 在区块链中，交易一旦发出就不可收回。
• Alice发出了一个3天后的交易，给Bob 1个比特币。
• 现在Alice反悔了，但是之前的消息不可撤回。
• Alice这时候发出一个没有Locktime的交易，把这个相同的比特币支付给Alice’。
• 这样当三天后这个给Bob的交易执行的时候会被认为是一个double spend因此会被拒绝
• Alice成功反悔了她之前的操作。

关于Locktime的使用:

• 如果locktime < 500 million. locktime被认为是block height (The number of blocks preceding a particular block on a block chain 就是说之后的第几个区块)。Transaction can be added to any block which has this height or higher.
• 如果locktime >= 500 million, 那locktime被认为是一个unix format的时间 (the number of seconds elapsed since 1970-01-01T00:00 UTC—currently over 1.395 billion). The transaction can be added to any block whose block time is greater than the locktime.

Multisig

The multisig can be implemented as a m of n scheme.

简单的应用如下: Alice, Bob, Tom把他们的bitcoin都放在一起，如果要使用必须要拿到至少两个人的签名。(就是个例子，不要考虑两人狼狈为奸坑掉第三个人…hhh)

Writing messages in a transaction

应用场景: 表白(偷笑), 因为区块链是永存的…也不能删除。所以把表白信息放在区块链上后就写入历史了！看，表白墙。当然也可以用于存在性证明，比如说我拍了个照片或者其他数字信息放到区块链中去就表示自己拥有它了(就像你拥有钱币一样样的意思)。

一个方法是用OP_RETURN

• This script allows 80 bytes of data to be added to an output
• This creates a provably unspendable output that the network recognizes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

"vout" : [
    {
        "value" : 0.00000000,
        "n" : 0,
        "scriptPubKey" : {
            "asm" : "OP_RETURN 636861726c6579206c6f766573206865696469",
            "hex" : "6a13636861726c6579206c6f766573206865696469",
            "type" : "nulldata"
        }
    },
    {
        "value" : 0.00200000,
        "n" : 1,
        "scriptPubKey" : {
            "asm" : "OP_DUP OP_HASH160 b8268ce4d481413c4e848ff353cd16104291c45b OP_EQUALVERIFY OP_CHECKSIG",
            "hex" : "76a914b8268ce4d481413c4e848ff353cd16104291c45b88ac",
            "reqSigs" : 1,
            "type" : "pubkeyhash",
            "addresses" : [
             "1HnhWpkMHMjgt167kvgcPyurMmsCQ2WPgg"
            ]
        }
    }
],

上面的”636861726c6579206c6f766573206865696469”就是“charley loves heidi”

相关资料:

• https://opreturn.org/
• https://bitcoin.stackexchange.com/questions/29554/explanation-of-what-an-op-return-transaction-looks-like
• http://www.cnblogs.com/studyzy/p/write-string-to-blockchain.html

这部分笔记主要记录一些相关概念

What is Software Architecture?

A software system’s architecture is the set of principal design decisions about the system.

Other Definitions of Software Architecture

• Perry and Wolf:
  • Software Architecture = { Element, Form, Rationale }
• Shaw and Garlan: Software Architecture involves:
  • The description of elements from which systems are built,
  • Interactions among those elements,
  • Patterns that guide their composition, and
  • Constraints on these patterns.
• Kruchten:
  • Software architecture deals with the design and implementation of the high-level structure of software.
  • Architecture deals with abstraction, decomposition, composition, style, and aesthetics.

Prescriptive VS Descriptive

• Prescriptive是梦想，预想的架构
• Descriptive是现实，实际的架构。

Architectural Degradation / Decay

Architectural drift VS Architectural erosion

• Architectural drift is introduction of principal design decisions into a system’s descriptive architecture that are not included in, encompassed by, or implied by the prescriptive architecture. 指的是在原先的设计上增加了一些新的东西，但是不会破坏原先的结构。
• Architectural erosion is the introduction of architectural design decisions into a system’s descriptive architecture that violate its prescriptive architecture. 这里会破坏原来设计的结构。

Architecture Recovery

Architecture recovery is the process of determining a software system’s architecture from its implementation-level artifacts.
就是根据已经实现后的效果来还原代码结构。一般根据源代码，可执行文件，类文件等。

其他概念

• Deployment 部署和上线 评估维度一般有 需要的内存，耗费的能源以及占用的带宽。
• Components: 组成元件
• Connectors: 负责components之间的链接和交互。
• Configurations: An architectural configuration, or topology. Is a set of specific associations between the components and connectors of a software system’s architecture.

本章主题 - 在区块链中使用的hash技术

什么是哈希

• 哈希: [Data of any size] —> [Hash Function] —> [Data of fixed size]
• 加密(Cryptography): 防止别人获取信息的一种科技。（注明，虽然哈希函数广泛用于加密技术，但是区块链中哈希函数的使用不是用于加密相关

SHA256

SHA(Secure Hash Algorithm) 是一种加密哈希函数类，由NSA发明。

常用于篡改检测 - 通过比较原始哈希值和当前哈希值来判断文件是否被篡改。

相对应的哈希又叫做digest(签名)。

SHA256就是这样的一种哈希函数

• It generates a 256 bit hash of 1s and 0s from the input string
• The 256 bits are stored as 8 32-bit words
• It as a 256 bit fingerprint of the original message

[注: 很容易想到SHA256是一个无穷到有穷集合的映射]

SHA256特性

• Deterministic： 相同的input一定产生相同的output
• Non-invertible: 已知hash值，没有办法得到input是什么
• Uniform: hash值一样的情况很低，唯一的方法是brute force。

由此引申出三个附加特性

• Collision resitance (碰撞阻力) - it is infeasible to find two inputs that yield the same hash.

• Hiding(隐蔽性) - 比如说Alice想给Bob传送一个信息，这个信息要么是Yes要么是No。这样这个信息其实很容易猜测，因为只有两个选择。在这个情况下我们希望输入来自于一个范围更大的集合。对应的应用是承诺(Commitment)，会在之后讲到。A hash function H is hiding if: when a secret value r is chosen from a probability distribution that has high min‐entropy , then given H(r ‖ x) it is infeasible to find x .

• Puzzle friendly(谜题友好) - Alice给Bob一个值B希望Bob找到值A,从而A和B组合的哈希值C满足某个特定结构比如说以20个0作为开头，这里的A叫做nonce, 在之后会说到这个概念。

这学期旁听了ITP499 blockchain一课。该博文是对应的学习笔记。

近年科学技术的发展

Digital(Computer)计算机 -> Network(TCP, Internet)互联网技术 -> Communication(Usenet, Email, Messaging)各类通讯工具 -> Web(Information, Ecommerce, Enterprise)Web技术电子商务 -> Mobile(Apps, Maps)手机应用,地图 -> Social(Media, Networks)社交网络技术 -> Data(Analysis, Machine Learning)数据分析 -> Crypto(Bitcoin, Blockchain, Smart contracts)加密技术,比特币区块链智能合约

随着计算机的诞生和互联网技术及相关应用的成熟和普遍，我们的生活的方方面面也在被改变。而2017年是比特币大火的一年，背后的区块链技术也开始进入大众的眼球。区块链会在哪些方面表现出重要影响，其背后的技术又是怎么样的，这些话题都值得专业人士甚至是普通人的关注。

什么是区块链

课上老师从三个角度来介绍了个概念。

从技术的角度(Techinical Definition)

A blockchain is a linked list that is built with hash pointers instead of regular pointers。

我们都知道普通指针是指向数据的位置，而哈希指针在此之外还增加了新的功能 - 保存了其位置数据的哈希值。这样用哈希指针连起来的列表，每个区块不仅可以告诉我们上一个区块的值在哪里还告诉我们了该值的摘要。

仔细的想一想这个特性可以很简单的做到防止篡改，因为对每个区块进行篡改都要改变下一个区块哈希指针的哈希值，因为该哈希指针也属于下个区块的一部分，所以也就是下个区块也进行了篡改，这样就需要修改下下个区块的哈希指针的哈希值，以此类推到最后一个使用的数据区块,那如果我们让指向最后一个区块的哈希指针无法修改，我们就达到了防止篡改的目的。这个位于链表头部的哈希叫做创世区块 - genesis block。

从财经会计的角度来看(Financial-accounting definition)

A blockchain is a public, distributed ledger of peer-to-peer transactions。

从这个角度，区块链是一个公开的，分布式的记录所有点对点交易记录的总帐。

社会经济学??的角度(Socio-political-economic-semi-technical libertarian definition)

A blockchain is an open, borderless, decentralized, public, trustless, permissionless, immutable record of transactions.

这个是从区块链的特点出发进行定义，点出了区块链的去中心化、公开透明，不可篡改，匿名性等特点。

关于去中心化，公开透明这些其实都有待商榷。拿去中心化这一点来说理论上并没有严格的纯中心化或者完全去中心化的产品。如电子邮件实质也是SMTP的去中心化系统，任何人愿意都可以设计一个自己的电子邮件服务器，然而实际情况是，只有一小部分电子邮件服务商在这个领域占领着统治地位。

货币的发展

货币形式的演变:

物物交换 -> 用贝壳龟壳等作为实物货币 -> 金属货币(国家铸造) -> 纸币 -> 银行卡信用卡 -> paypal等 -> 加密货币

推荐文章:
货币新形态-金融创新与货币演变

货币的功能与比特币:

无论是哪个时期的货币，货币总要满足以下三个功能:

• store of value[价值储藏], which means people can save it and use it later—smoothing their purchases over time;
• unit of account[价值尺度], that is, provide a common base for prices; or
• medium of exchange[支付手段], something that people can use to buy and sell from one another.

比特币满足这三个条件，因此它可以作为一种货币来使用。

最后一学期决定旁听Software Architectures 这门课。课程老师是“Software Architecture: Foundations, Theory, and Practice”一书的作者之一 - Nenad Medvidovic。课程网站见链接。

What is the Big Idea:

The big idea is that software architecture must be at the very heart of software system design and development.

An architecture-centric approach to software engineering places an emphasis on design - design pervades the engineering activity from the very beginning.

Software Engineering Difficulties:

Software engineers deal with unique set of problems.

Some problems can be eliminated - “accidental difficulties”

Some problems can be lessened, but not eliminated - “essential difficulties”
如:

• Complexity
• Conformity(一致性,便于用于不同的操作系统 )
• Changeability(易于修改的,有延展性的)
• Intangibility(软件是无形的，它不像建筑一样有一定的几何结构以及满足一定的物理规律)

Analogy: Architecture of Buildings

显而易见的共同点：

• Satisfaction of customers’ needs
• Specialization of labor
• Multiple perspectives of the final product
• Intermediate points where plans and progress are reviewed

更进一步的相似点有:

• Architecture is different from, but linked with the product/structure
• Properties of structures are induced by the design of the architecture
• The architect has a distinctive role and character
• Process is not as important as architecture
• Architecture has matured over time into a discipline(架构成为一门学科)

  Architectural styles as sets of constraints.
  Styles also as wide range of solutions, techniques and palettes(调色盘) of compatible materials, colors and size. 即根据不同的条件和情况选择不同的styles.

不同之处和类比的局限性有:

• We know a lot about buildings, much less about software
• The nature of software is different from that of building architecture
• Software is much more malleable(具有延展性) than physical materials
• The two “construction industries” are very different = =建筑工人和程序员的工作环境差别很大hhh
• Software deployment has no counterpart in building architecture
• Software is a machine; a building is not.
• 我们可以比较容易的看出房屋的架构(比如说在房子里面走走量量就可以画出来这个房子的设计图)而对于一个软件来说，看出其结构是很难的。

举例1: The Architecture of the Web

What is the Web?

In one view, focusing on the user’s perception, the Web is a dynamic set of relationships among collections of information.

In another view, focusing on coarse-grained aspects of the Web’s structure, the Web is a dynamic collection of independently owned and operated machines, located around the world, which interact across computer networks.

In another view, taking the perspective of an application developer, it is a collection of independently written programs that interact with each other according to rules specified in the HTTP, URI, MIME and HTML standards.

下面我们从架构的角度来介绍Web.

• The Web is a collection of resources, each of which has a unique name known as a uniform resource locator, or “URL”.
• Each resource denotes, informally, some information.
• URI’s can be used to determine the identity of a machine on the Internet, known as an origin server, where the value of the resource may be ascertained.
• Communication is initiated by clients, known as user agents, who make requests of servers.
• Web browsers are common instances of user agents.
• Resources can be manipulated through their representations.
• HTML is a very common representation language used on the Web.
• All communication between user agents and origin servers must be performed by a simple, generic protocol (HTTP), which offers the command methods GET, POST, etc.
• All communication between user agents and origin servers must be fully self-contained. (So-called “stateless interactions”)

前面两个角度介绍的实在是太泛泛了,所以我们只与最后一个角度相比较。
按照这个思路来解释上面那个图(developer view那个)就容易很多了。

Documents A to G are resources; machines machine.uci.edu and machine.usc.edu running the Apache Web server are example origin servers. User agents could be personal laptops running a Web browser such as Internet Explorer. Representations include a copy of the HTML of Lewis’s biography, and a JPEG of the current view of The Kilns as imaged by a webcam.

举例2: 从Architecture的角度来看一个Unix Shell应用

1

ls invoices | grep -e August | sort

This application creates a sorted list of all the files in the directory named invoices whose names include the character string “August”.

为了理解这个应用, 我们只需要知道filter是什么, 该应用中的每一个filter的作用是什么, 什么是pipe, pipe 是如何连接这几个filter的就可以了。

此外,根据这个例子我们可以总结出一个architectural style - “pipe-and-filter”, 并且运用到更多的情景当中。

举例3: 在产品线和产品系列上的运用

有这样一个情景:
客户可能有这些不同的需求

• a 35-inch HDTV with a built-in DVD player for the North American market.
• a 35-inch HDTV without the DVD player
• a 35-inch HDTV with a built-in DVD player for the European market

这些产品互相不同但是又有相同的组成部分。那为了满足客户的各种需求，制造商就要考虑Reusing structure, behaviors, and component implementation了。

Reusing 好处多多:

• Simplifies the software development task
• Reduces the development time and cost
• Improves the overall system reliability
• Concrete manifestation of the company’s corporate experience, knowledge, and competitive advantage. 结构化的产品往往需要公司的部门也结构化，这样新产品的诞生将不再依赖过度依赖于员工的经验。尤其对于员工流动性大的公司来说是大有益处。

研究生的最后一个学期决定选一门叫做immersive environment的课程，课程又叫做Augmented, Virtual & Mixed Reality。此前从未接触过相关的知识，技能为0。带着一颗乐观积极向上的野心，我义无反顾的打开了新世界的大门。

感兴趣的应用

课程最终需要做出一个VR或者AR的应用。于是在这里搜集了一下现有的，我比较喜欢的或者觉得有趣的项目。以供参考。

资源

Unity Store

FusedVR Youtube Channel

Road to VR - VR资讯分享网页

设备

technology must be used to liberate the individual.

很早就听说过Bitcoin(比特币)这一概念但是一直没有深入了解的想法。大概因为我这个老古董对于新生的事物总是心存胆怯，稍微有一点点出格的大变动就觉得地球要毁灭。今天无意间看到了BBC的纪录片-The Rise and Rise of Bitcoin。已经是2014年的老片子了，便决定花半个下午好好观看一下也作为区块链的背景资料。也在博客开了一个区块链的坑，希望以后常种草。

以下是纪录片内容的摘录和整理

比特币(Bitcoin)的由来

那个叫中本聪的人发明了比特币，起稿了比特币白皮书。却没有人知道谁是中本聪。

在2008年万圣节，某人用化名中本聪在密码学邮件组发帖。帖子中指向的白皮书提出一种用于互联网的新型支付系统。内容包含使用“点对点网络系统”的协议，工作量证明以及公钥加密。

虽然在这之前的很多年以来，计算机行家们都在尝试用这些技术创造数字货币。但是中本聪创造了这种史无前例的融合方法。所以说他发明了比特币。

比特币(Bitcoin)的发展

中本聪的设计得到了广泛的认可，于是世界的程序员和密码学家开始着手共同发展比特币。在2009年10月,第一个汇率发布了，标记1美元可以兑换1309个比特币。比特币那时候很便宜,而后几年里，它们的兑换交易依旧以美元的分厘计算。

2010年春季,一个叫做赖斯罗(Laszlo)的佛罗里达伙计决定试着用他的比特币买东西，他报价10000枚比特币给那个愿意买披萨给他的人。一个在伦敦的人接受了报价并且打了一个长途电话在Papa John’s家定了两个披萨。人们认为这是首个比特币兑换实物的交易。

为了让比特币兴盛起来，需要更多的人拥有比特币。于是，日本一个叫做“门头沟”的比特币交易所应运而生。比特币交易额开始上升，到2010年11月已挖出的比特币大概四百万枚，交易价格已经到了0.5美元一枚了。市场苏醒，比特币看起来开始有成为货币的潜质了。

在一次25万件政府公文被公布于众后，维基解密的捐款渠道都被切断 - 像美国银行，以及visa和万事达信用卡更不用说贝宝和西联汇款了。一篇在“pc世界”上的文章建议可以利用比特币来给维基解密捐助。中本聪最后发布的一些帖子里就有对于这个文章的回复。他说”要是能任何别的场合下能获得此等关注就好了，维基解密踢翻了马蜂窝，蜂群却向我们扑来”。不久之后，中本聪从论坛中销声匿迹。

两个月后丝绸之路（silk road）建立，它是一个用来交易毒品 以及其他非法东西的黑色市场。只能用比特币，因为比特币让金钱流向基本上不可能得到追踪。

比特币的汇率持续上涨，到了2011年2月份比特币的价格已经到达每枚1美元，这吸引了大量用户以及投机者，到六月的时候，价格暴涨到了31美元，然后突然崩溃了。市场重挫, 门头沟被黑了，在之后很长一段时间里这都打击着投资者的信心，价格一直下跌，到十月份只有2美元左右。

金融危机在塞浦路斯爆发。2013年4月份。欧盟和德国打着反洗钱的幌子，通过对存款人增税的方式来应对塞浦路斯的债务危机。塞浦路斯的储户人人自危，比特币作为去中心化和超主权的网络货币得到了欧洲避险资金的青睐。

塞浦路斯危机发生的同时，美国财政部的监管人员也在思量着比特币。美国金融犯罪执法网络发布了首个对于虚拟货币的监管条例，条例中隐射道就它本身而言,比特币不是非法的。

塞浦路斯事件使人们意识到比特币可以作为一个金融安全的天堂。美国监管者的点头对投资者来说更是亮了绿灯。交易价格继续爬升。比特币开始从非常非常早期的投资阶段进入到相对早期的投资阶段。

Bitinstant

2011年，23岁的Charlie shrem创立了Bitinstant。Bitinstant是比特币界的第一个初创企业。在比特币早期,人们必须辗转很多个地方才能买到它。唯一捷径就是去门头沟交易所了，但这个过程需要在数个中间机构之间汇钱，要花费数周。查理成立Bitinstant为的就是简化这个过程帮人们快速买币。

2014年，Charlie Shrem和他的客户Robert Faiella承认了与无执照货币交换相关的指控。 他们在年初被捕，被控参与了超过100万美元的比特币交易，检方称他们明知用户购买比特币是去丝绸之路购买毒品。Charlie Shrem被判了两年的牢狱。

不同人士对比特币的看法

美国金融犯罪执法网络的部门人员对于比特币监管条例，表明了看法:如果你是一个用比特币来购买产品和服务的消费者,那么，那监管条例将跟你没关系。它主要是为了防范金融系统里的洗钱以及恐怖主义援助。我觉得肯定–比特币社区里的很多人都担心比特币会被用作不好的用途。它还有很多巨大的潜力，如围绕比特币和虚拟经济的技术革新。比特币在无银行地区确实有很大的潜力能够真的提供方便的服务。但另一方面来看它是金融系统的一部分了，包括全美，全球金融系统的一部分。当然它就得负责任了，责任就包括不让某些机构用它来从事犯罪以及恐怖主义。

纪录片中Mike Caldwell(实体比特币-casascius币)的创造者说:密码学其实能为我们做很多事情,像很多社会问题都能被密码学解决。密码学能给选举带去公正，常人是难以理解密码学的，毕竟大多数人水平不足。

纪录片录制者丹尼尔说:现在我们只通过比特币来发送金钱,但是很多人相信，它的革命性意义不仅如此。比特币背后的技术可以被用来创建无法作假，规定不可改动的去中心化系统。

视频链接

比特币的崛起

该博文是命题逻辑和一阶逻辑的学习笔记，总结了教材和老师讲义。请勿转载。
之后可能会附上相关代码。

近期上搜索引擎的时候提到了知识图谱这个专题，先开坑。后续慢慢填。